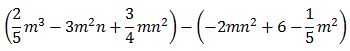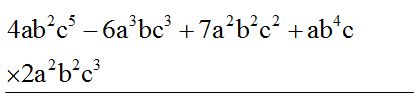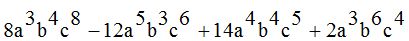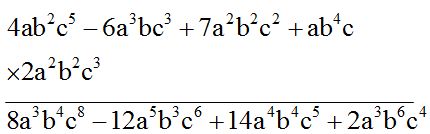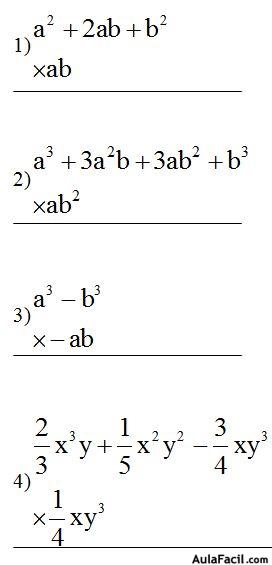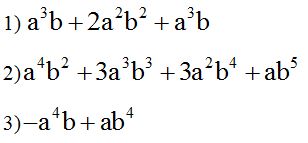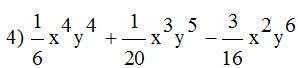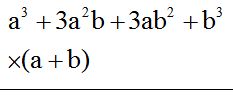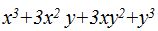Álgebra, para definirla de un modo sencillo,
diremos que es la rama de las matemáticas en la que se usan letras para
representar relaciones aritméticas.
Tal como ocurre en la
aritmética, las operaciones fundamentales del álgebra son adición, sustracción,
multiplicación, división y cálculo de raíces.
La aritmética, sin embargo,
no es capaz de generalizar las relaciones matemáticas, como el Teorema de Pitagoras,
que dice que en un triángulo rectángulo el área del cuadrado cuyos lados son
iguales a la hipotenusa es igual a la suma de las áreas de los cuadrados
cuyos lados son iguales a los catetos.
La aritmética sólo da casos
particulares de esta relación (por ejemplo, 3, 4 y 5, ya que (3 2 ) 9 + (4 2 ) 16 = (5 2 ) 25). El
álgebra, por el contrario, puede dar una generalización que cumple las
condiciones del teorema: a 2 +
b2 = c2.
Un número multiplicado por sí
mismo se denomina cuadrado, y
se representa con el superíndice 2. Por ejemplo, la notación de 3 × 3
es 3 2; de la
misma manera, a × a es igual que a 2.
El álgebra clásica, que se
ocupa de resolver ecuaciones, utiliza símbolos en vez de números específicos y
operaciones aritméticas para determinar cómo usar dichos símbolos.
El álgebra moderna ha
evolucionado desde el álgebra clásica al poner más atención en las estructuras
matemáticas.
Los matemáticos consideran al
álgebra moderna como un conjunto de objetos con reglas que los conectan o
relacionan. Así, en su forma más general, una buena definición de álgebra es la
que dice que el álgebra es el idioma de las matemáticas.