Es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
Ejemplo: 2x2 y3
Por lo tanto dicho coeficiente tiene sus partes,las cuales ¡¡te mostraremos!!
Coeficiente
El coeficiente del monomio es el
número que aparece multiplicando a las variables.
número que aparece multiplicando a las variables.
Parte literal
La parte literal está constituida
por las letras y sus exponentes.
por las letras y sus exponentes.
Grado
El grado de un monomio es la suma
de todos los exponentes de las letras o variables.
de todos los exponentes de las letras o variables.
El grado de 2x2 y3 z es: 2 + 3 + 1 = 6
Monomios semejantes
Dos monomios son semejantes cuando tienen
la misma parte literal.
la misma parte literal.
2x2 y3 z es semejante a 5x2 y3 z
Suma de monomios
Sólo podemos sumar monomios semejantes.
La suma de los monomios es otro monomio
que tiene la misma parte literal y
cuyo coeficiente es la suma de los coeficientes.
que tiene la misma parte literal y
cuyo coeficiente es la suma de los coeficientes.
axn + bxn = (a + b)xn
2x2 y3 z + 3x2 y3 z = 5x2 y3 z
Si los monomios no son semejantes
se obtiene un polinomio.
se obtiene un polinomio.
2x2 y3 + 3x2 y3 z
Para restar monomios es necesario que sean semejantes. Monomios semejantes son aquellos que tienen la misma parte literal y el mismo grado.
Se restan monomios semejantes, sumando al minuendo el opuesto de cada término semejante del sustraendo:
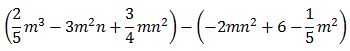
Colocando detrás, los términos del sustraendo que no tienen semejantes.

Resta de monomios
La resta de monomios es muy parecida a la suma, sólo que hay que cambiar los números del sustraendo por su simétrico y se resuelve aplicando las reglas de la suma.
Ahora bien, si tomamos en cuenta que el valor absoluto de un número algebraico es el valor de dicho número sin tener en cuenta su signo.
Ejemplo: si tenemos (8x) – (6x) =
a) Se convierte la resta en suma cambiando el sustraendo por su simétrico.
(8x) + (-6x) =
b) Se resuelve aplicando las reglas de la suma.
(8x) + (-6x) = (8-6) x = +2x
PARA ELLO ES MUY NECESARIO
QUE RECORDEMOS LA LEY DE LOS SIGNOS,
ASÍ QUE INGRESARE UN VÍDEO
DONDE LO RECORDARAS CON FACILIDAD
QUE RECORDEMOS LA LEY DE LOS SIGNOS,
ASÍ QUE INGRESARE UN VÍDEO
DONDE LO RECORDARAS CON FACILIDAD
No hay comentarios.:
Publicar un comentario