En álgebra, la división de polinomios es un algoritmo que permite dividir un polinomio por otro polinomio que no sea nulo. . El algoritmo es una versión generalizada de la técnica aritmética de división larga. Este tema es un poco extenso, una de ellas es la forma de realizar la operación, saber identificar cada una de las divisiones

Es fácilmente realizable a mano, porque separa un problema de división complejo, en otros más pequeños.
La división de un polinomio por un número es otro polinomio que tiene
- El mismo de grado
- Sus coeficientes resultan de dividir cada uno de los coeficientes del polinomio entre el número
- Se dejan las mismas partes literales.
EJEMPLOS DE DIVISIONES DE POLINOMIOS :

VIDEOS DE APOYO:
VIDEO 1
VIDEO 2
VIDEO 3
El método que te voy a explicar, corresponde al método general de división de polinomios, ya que existen más métodos para dividir polinomios, como por ejemplo el método o la regla de Ruffini, que veremos más adelante.
Este método sirve para dividir cualquier tipo de polinomios y para realizarlo hay que tener en cuenta las propiedades anteriores.
Vamos a verlo con un ejemplo paso a paso:

El primer paso consiste en colocar y escribir correctamente el dividendo y el divisor para poder empezar su división.
En nuestro caso, el numerador es el dividendo y el denominador es el divisor.
Tanto el dividendo, como el divisor, los términos se escriben en orden decreciente de los grados de sus términos, es decir, empezando por el de mayor grado, hasta llegar al término de grado 0 (el término independiente).
En nuestro ejemplo, el dividendo no tiene término de grado 2, por lo que dejamos un espacio en su lugar. Nos queda así:

Una vez tenemos en su sitio el dividendo y el divisor, y con los correspondientes huecos de los términos que faltan, vamos a empezar a calcular el cociente.
Para ello, dividimos el primer término del dividendo entre el primer término del divisor:


Y lo colocamos en el cociente. Corresponde al primer término del cociente:

Ahora, debemos multiplicar este término del cociente por cada uno de los términos del divisor:

Los colocamos debajo del dividendo, pero cumpliendo éstas dos condiciones:
- Cada uno se coloca debajo de su término semejante, es decir, del término tenga el mismo grado o de su hueco correspondiente (en el caso de que el dividendo no tenga término de ese grado)
- Con el signo contrario
Nos queda de la siguiente manera:
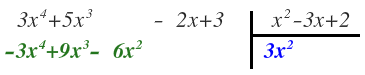
Como dejamos un hueco para el término de grado 2, el 6x² lo colocamos debajo de ese hueco.
Y ahora en el dividendo, sumamos verticalmente las dos expresiones que tenemos:

Al tener cada término debajo de su término semejante del dividendo, esta suma se realiza de manera más ordenada. Es lo que buscamos también cuando dejamos el hueco en el dividendo del término que falte.
No hay comentarios.:
Publicar un comentario