Se coloca el polinomio como multiplicando y el monomio como multiplicador y seguidamente multiplicamos el monomio por cada término del polinomio.
Debes tener en cuenta:
1.- La ley de los signos.
2.- Producto de potencias de la misma base se suman los exponentes.
- Calcula el producto siguiente:
Solución:
- Calcula:
Respuestas:
PRODUCTO DE UN POLINOMIO POR OTRO POLINOMIO.
a) Escribes el multiplicando y debajo el multiplicador y trazas una raya por debajo de estas dos líneas.
b) Multiplicas cada término del multiplicador por cada uno del multiplicando. Primero multiplicamos por ‘a’ a cada término del multiplicando, comenzando por delante (de izquierda a derecha)
c) Cuando acabas de multiplicar el primer término del multiplicador por cada uno del multiplicando pasas a otra línea más abajo y en ésta, vas colocando los resultados haciendo coincidir los términos semejantes. Pasamos a multiplicar por ‘b’ a cada término del multiplicando, comenzando por delante (de izquierda a derecha)
d) Trazamos una raya horizontal y sumamos los términos semejantes comenzando por la izquierda:
- Multiplica (x+3) por (x+5):
Solución:
- Multiplica (2x-5)(3x-2)
Solución:
Solución:
Solución:
- Multiplica (a+b+c)(a+b-c)
Solución:
Ten en cuenta: 1) Guarda el orden alfabético de la parte literal
después de calcular el producto
2) Coloca los términos semejantes en la misma
columna y si no coinciden escribe el término calculado más a la derecha.
- Multiplica (a – b – c)(a – b + c)
Solución:
Respuesta:
Solución:
Recuerda que si no encuentras términos semejantes colócalos a la derecha de la última columna. No importa que en todo el proceso del producto no hayas encontrado términos semejantes.
- Multiplica (a + b)(a + b)(a + b)
Solución:
- Primero multiplicamos los dos primeros factores.
- Al resultado obtenido del paso anterior lo multiplicamos por el tercer factor:
- Primero multiplicamos los dos primeros factores.
- Al resultado obtenido del paso anterior lo multiplicamos por el tercer factor:
- Multiplica (a + b + c) (a + b – c) (a – b – c )
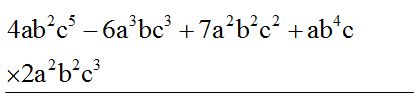
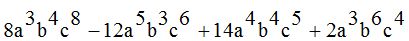
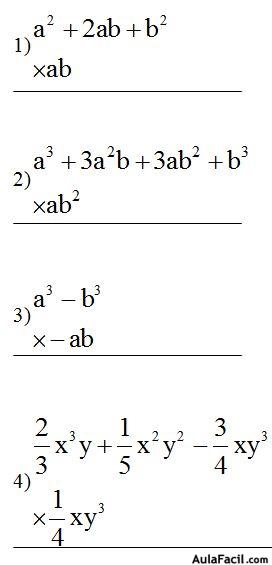
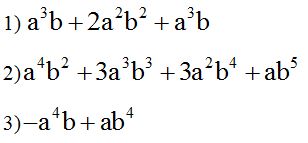
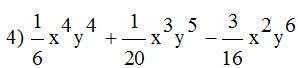
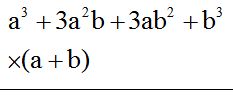
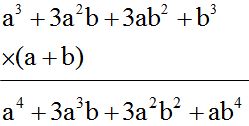
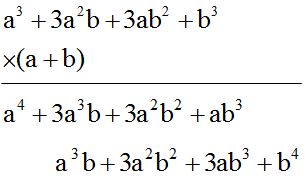
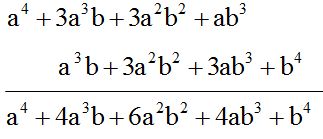
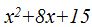
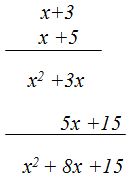
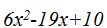
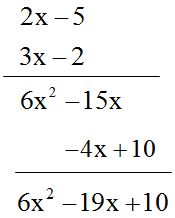
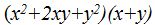
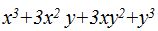
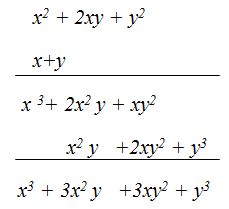
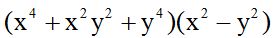
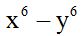
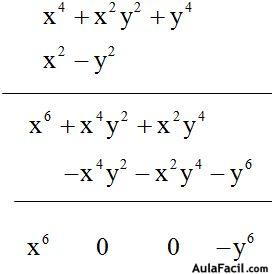
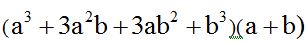
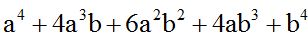
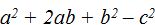
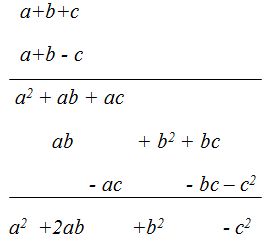
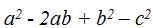
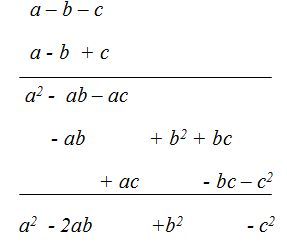
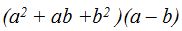
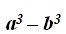
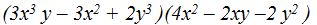
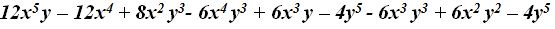
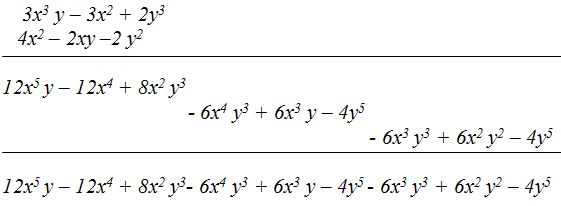
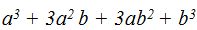
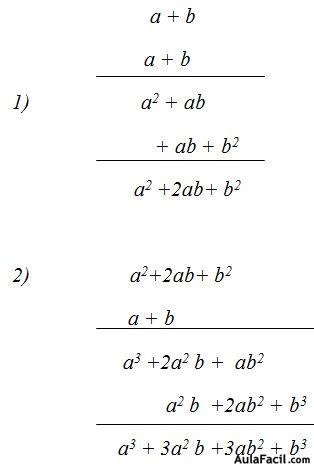
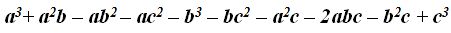
No hay comentarios.:
Publicar un comentario